by Yves Konigshofer

Payout Rate

The payout rate refers to the percentage of a bet that is returned, on average. If the payout rate exceeds 100%, then one would be expected to have net winnings in the long run. However, payout rates are usually below 100% and one is expected to lose money in the long run. A typical game in a casino will have a payout rate in the mid 90’s. This ensures that people will keep playing while making money for the casino. The payout rate can be calculated by multiplying the odds of winning a prize by the amount of that prize and dividing the result by the amount that must be bet. If there are multiple prizes that can be won with the same bet, then the payout rates for the individual prizes are added together.

Not counting the Jackpot, the payout rate for Mega Millions is around 18%. With the minimum $12 million Jackpot, the payout rate is a mere 25%. Thus, the payout rate for Mega Millions is typically much worse than what one encounters in a casino. However, as the Jackpot grows, the payout rate increases.

When is the Payout Rate Above 100%?

The odds of winning the Mega Millions Jackpot are 1/175,711,536. Dividing 82% by this leads to a Jackpot of about $144 million that is needed to have a payout rate around 100%. However, this does not take into account the fact that other people are playing and, if more than one person wins, then the Jackpot will be split and the payout rate will be much lower.

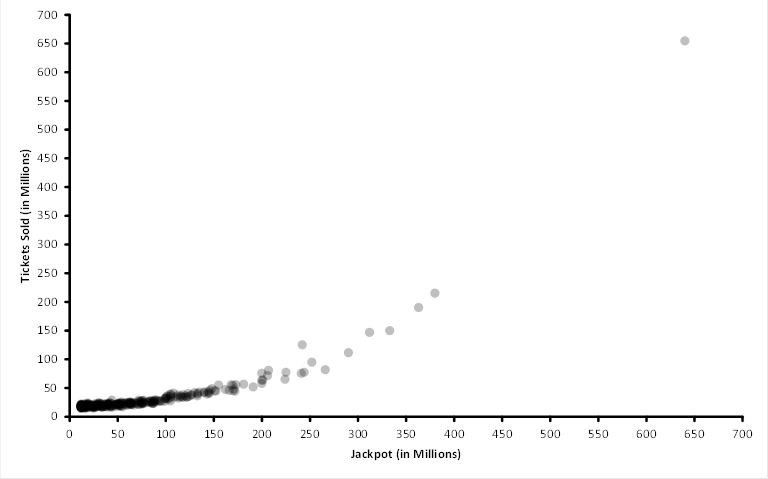
Tickets Sold

Mega Millions does not publish the amount of tickets sold for a given drawing. However, this can be approximated my multiplying the $2 prize winners (the most common prize) by 75, where 1/75 are the odds of winning that prize. Using data from 4/14/2009 through 5/15/2012 leads to the plot below, where it becomes clear that the higher Jackpots lead to more tickets being sold.

$Description: C:\Users\Yves\Documents\MegMill_files\image001.png$

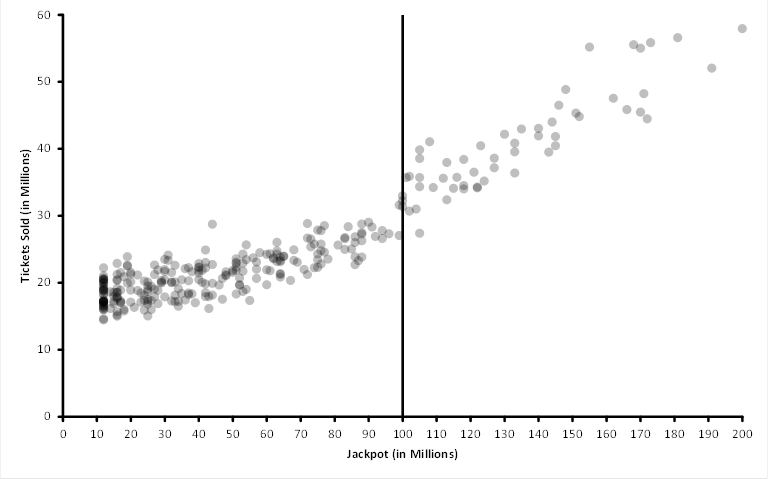
The $100 Million Effect

An interest effect is observed once the Jackpot grows to about $100 million. About 5-10 million more tickets are sold. This may be due the psychological effect of seeing a three digit Jackpot.

$Description: C:\Users\Yves\Documents\MegMill_files\image002.png$

The Expected Number of Jackpot Winners

The expected number of Jackpot winners can be obtained by multiplying the number of tickets sold by the odds of winning the Jackpot. The plot below shows that as the Jackpot grows in size, the number of expected winners increases exponentially.

$Description: C:\Users\Yves\Documents\MegMill_files\image003.png$

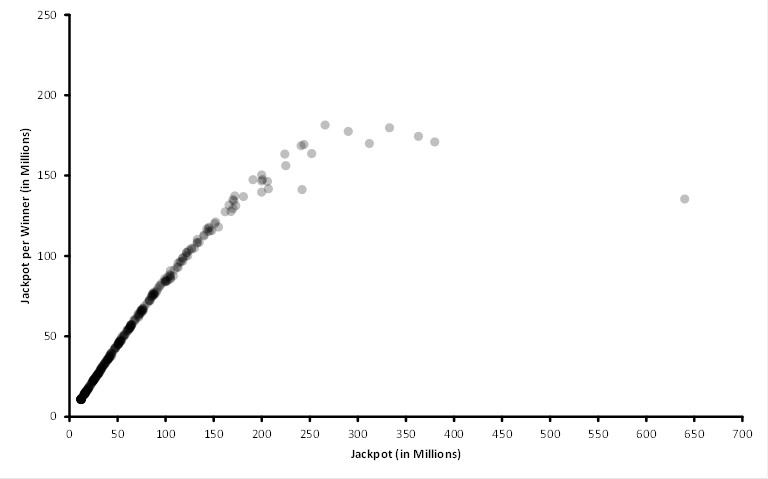
The Jackpot per Winner

By dividing the Jackpot by the expected number of winners, it is possible to approximate the amount of the Jackpot that would be won by a single person. Interestingly, for Mega Millions, this reaches a maximum around $200 million because of the exponential increase in the number of tickets sold as the Jackpot increases. For the 3/30/2012 record $640 million Jackpot, the expected Jackpot per winner was only $135 million (more than 2 tickets were sold for every person living in the US).

$Description: C:\Users\Yves\Documents\MegMill_files\image004.png$

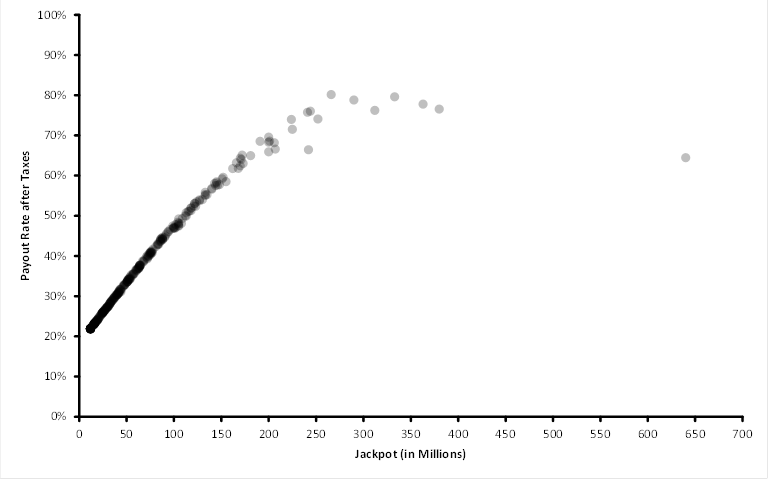
When to Play Mega Millions

Using the Jackpot per winner values, it is possible to calculate the payout rate for Mega Millions for a given Jackpot. This leads to the plot below and shows that the payout rate can be above 100% once the Jackpot grows above $185 million. Note that the payout rate appears to decrease once the Jackpot reaches $300 million.

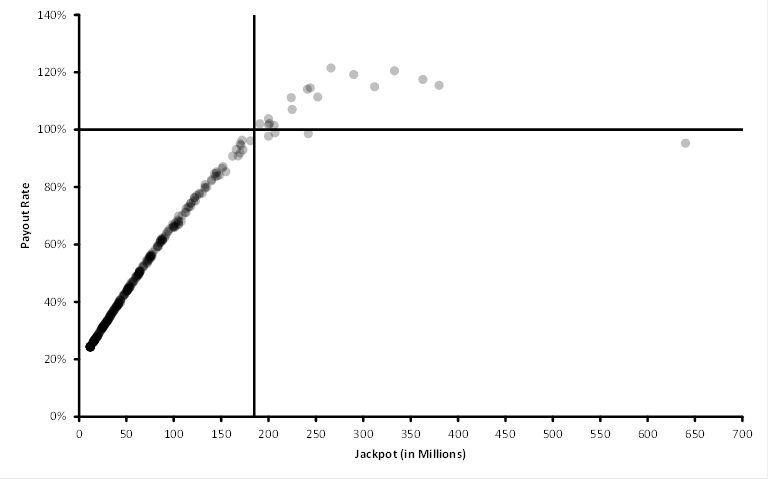
$Description: C:\Users\Yves\Documents\MegMill_files\image005.png$

Thus, if you are going to play Mega Millions, it only makes sense to do so once the Jackpot reaches about $185 million (and perhaps not if it climbs far above $400 million). However, for the Jackpot to make it to $185 million, it takes the efforts of all those people who are willing to play even when the payout rate is below 25%. Also, if one factors in that state and federal taxes may only leave one with less than 60% of the winnings, then the maximum payout rate would be about 80% – so, it would not make sense to play… but you can only win if you play…

$Description: C:\Users\Yves\Documents\MegMill_files\image006.png$